ニューマチックバルブスプリング

　2002年にMOTO-GPが始まり、アプリリアがニューマチックバルブスプリング(PVS)エンジンのマシンを走らせたが、競争力は低くPVSが注目されることはなかった。そして、2006年にスズキがV型4気筒エンジンにPVSを採用、MOTO-GPの排気量が800cc以下となった2007年にはカワサキもPVSエンジンをシーズンを通して使用、シーズン終盤にはヤマハもPVSエンジンを特定のレースで使用、PVSが注目を集めることになった。

1　通常のバルブ作動系

まず、通常のコイルスプリングを使用するバルブ作動系を見てみる。「カムでバルブを開け、バルブスプリングで戻す」といわれているが、そんなに単純なものではない。  一般にバルブの位置、速度、加速度の関係は図のようなものである（｢自動車用ガソリンエンジン設計の要諦｣（石川義和、山海堂2002)から引用)。言うまでもなく、位置を時間で微分したのが速度で、速度を微分したのが加速度である。図中の｢スプリング反力｣はスプリング反力による加速度である。 　なぜ、このような関係かは、「電車が発進し駅から離れ停止しまた駅に戻る」ことを想定してみれば分る。例えばカムが最大リフト時は、バルブの速度がゼロになっている。電車でいえば駅から最も離れた位置にいるのは、ブレーキを掛け終わり速度がゼロになり逆方向に発進しようとしている時である。 　電車でいえばブレーキを掛け、さらに逆方向に加速する、つまり負の加速度を生み出すのがバルブスプリングの役割である。図ではスプリング反力による負の加速度がカムの負の加速度より大きい（絶対値)のでバルブはカムから浮かない。 　しかし、バルブスプリング反力による負の加速度がカムの負の加速度より小さければ、カムがバルブを開けている行程ですらバルブがカムから浮いてしまう（バルブジャンプ)。カムの加速度は回転数の2乗に比例するので、必要なスプリング反力も回転数の2乗に比例して大きくなる。

また、スプリングの固有振動数とカムによる入力振動数が整数倍で一致すると共振し、スプリングが激しく伸縮する（バルブサージング)。2段ピッチスプリング等により抑制したとしても動的スプリング反力は変動し、右図のように、単純計算より早くバルブジャンプを起こすようになる（「直動式動弁系の動的解析によるバルブジャンプ予測」（三菱自動車テクニカルレビュー　2007No19)から引用。図中、左側の黒矢印の指示先は黄線の誤り。また、図中の「荷重」は本頁内では「反力」としている）。 2　ニューマチックバルブスプリング 　レーシングエンジンではどの程度の負の加速度が生じているのだろうか。某社の1998年型3リッター10気筒F-1エンジン（PVS)のデータ（｢サムライエンジニア｣(日高義明、スタジオ タック クリエイティブ2007))から計算する。 　吸気バルブ径39.5mm、吸気バルブリフト13.5mm、吸気バルブの最大負加速度30mm/rad2 　15000rpm時(カムシャフトは7500rpm)の加速度（重力加速度比)は 　30×(2×円周率×7500/60)2/(1000×9.81)=1890G 　17000rpmでは2430Gとなる。

　本エンジンの吸気バルブ1本あたりの慣性質量（コッター、スプリング等を含む)を100gとすれば、バルブを2430Gで動かすためには、

　2430×100/1000＝243kgf

の力が必要である。本エンジンの最大リフト時のスプリング反力は250kgf程度ということだが、この反力は、コイルスプリングでは達成困難な数字である。

PVSの構造は右図（http://www.pureluckdesign.com/ferrari/f1engine/から引用)のようになっている。図中のピストンの下側が高圧空気（または高圧窒素）で満たされており、これがスプリングの役割を果たす。各部の剛性・強度が保たれる限り、空気（又は窒素）の圧力を高めることにより必要な反力を得ることができる。 　このようにPVSの第一のメリットは、 (1)少ないスペースでコイルスプリングより大きな反力が得られる。 ことにある。そして、 、 （2)バルブ周りをコンパクトにすることができ、コイルスプリングも不要になる。往復部分質量が小さくなり、必要スプリング反力も小さくなる。 (3)スプリングの共振をあまり考慮する必要がない。回転数が同じならコイルスプリングより必要スプリング反力が小さくなる。 　この結果、(1))〜(3)のメリットにより、バルブ加速度大の方向である ・高回転 ・大バルブリフト ・大バルブリフト増加率(バルブリフト/回転角） に大きな効果がある。また、(2)、(3)により、バルブ加速度が同じであったとしても、摩擦損失（フリクションロス)の低減に大きな効果があるが、摩擦損失全体に占めるバルブ作動系の比率は小さい（備考参照）。

一方で、コイルスプリングとは圧縮特性が異なり、指数関数で圧力が増加することに留意が必要である。右図でコイルスプリングの特性は黒線、PVSの特性は赤線である。最大リフト時のスプリング反力はPVSがコイルスプリングを20％程度上回っているが、中間リフトでは同等以下になってしまっている。中間リフトでもバルブジャンプを起こす可能性は十分あり、PVSで中間リフト時に合わせてスプリング反力を設定すると、最大リフト時のスプリング反力は無駄に大きくなってしまうので、上記(2)、(3)のメリットもある程度は相殺される。 　また、PVSでは回転数が下がった時に空気圧（または窒素圧）を低下させ、カム駆動の摩擦損失を低減できることもメリットといわれており、この技術に関する特許出願も行われている。ただ、このようにすると空気（または窒素）の流出量が増加するので、小さな蓄圧タンクだけで1レースを持たすことは難しいように思う。 　2006年型のヤマハYZR-M1の最高回転数を17000rpmとするなら、上記F-1エンジンと同程度だが、気筒あたり排気量がF-1エンジンの300ccに対して247ccと小さいので吸気バルブ径・質量も小さく、必要バルブスプリング反力は小さい。ただ、2005年型YZR-M1は 　2004年型(後期型)と比べ吸気バルブ径を大きくしたにもかかわらず、吸気バルブリフトを小さく（加速度小の方向)せざるを得なかった（自動車技術会2006春季学術講演会(2006.5))

ことから分るように、すでにコイルスプリングの限界を超えていた。

   そして、MOTO-GPが990cc時代だった2006年以前はスロットルを全開にすることは少なかったが、800ccとなりスロットル全開時間が長くなることにより、PVSのメリットが浮き彫りにされることになったのである。

備考 　右図はヤマハが公開した資料で、左が2007年型YZR-M1、右が2008年型YZR-M1の最高出力時摩擦損失の内訳を示しており、 バルブ作動系の摩擦損失が摩擦損失全体に占める比率は1/15程度 である。「レーシングマシンの燃費」で試算したように、2007年型YZR-M1の最高出力時摩擦損失を5.8kgｆ・mとすると、バルブ作動系の摩擦損失による出力損失は、最高出力発生回転数を17000rpmとして、 5.8×17000/(15×716.2)＝9.2PS 程度である。これが少々変化したところで、出力の点では高バルブリフト化等ほどのメリットではない。

3　デスモドロミックバルブ作動系

　ドゥカティが使用しているデスモドロミックバルブ作動系（強制開閉バルブ)の概略構造は下右図（http://diem1.ing.unibo.it/mechmach/rivola/pub38.pdf　から引用。現在はリンク切れのため「Multibody Analysis Of The Desmodromic Valve Train Of The Ducati Motogp Engine」で検索されたい）のとおり、通常のカムとは別のカム（図中Conjugate camの奥側のカム)でバルブに負の加速度を与えている。 そして

「通常のバルブスプリング使用エンジンではカムを手で回すことができないが、デスモドロミックエンジンではカムを手で回すことができる。デスモドロミックはフリクションロスがほんどない」   といわれているが、この考え方は間違っている。 　通常のコイルスプリング使用エンジン（以下「バルブスプリングエンジン」)でカムを回すことができない理由の多くは摩擦損失（フリクションロス）ではなく、カムを回すとバルブスプリングを圧縮するからである。バルブスプリングを圧縮して溜められたエネルギーはバルブスプリングが伸びることで回収される。カムを回す時の手応えの差が摩擦損失の差ではない。 　もちろん、バルブがカムに強く押し付けられれば摩擦損失が増大するが、そもそもバルブスプリングエンジンのスプリング反力はバルブに加速度を与えるために設定されているのであり、デスモドロミックでもカムが（ロッカーアーム/スイングアームを介して）バルブを加速すれば、バルブがカムに押し付けられる。 　そこで、バルブがカムシャフトに押し付けられる力とその時間の積（FD)が回転数によってどう変わるか見てみる。

　

バルブスプリングエンジンでは、右図の １ + 2 + 4 + 5 + 6 + 7  の部分の面積がFDになる。3が関係ないのは、スプリング反力の方向と同じ方向の加速度でカムが動くからである。そして、回転数が低下すれば3が減少し6、7が増大し、回転数が上昇すれば3が増大し6、7が減少する。 　もちろん、回転数の変化に伴い1、2、4、5も変化するが、FDだけでなくカム半径も考慮する必要があり、1、2、4、5より3の方がカム半径※が大きく、この領域で3が増大することによりバルブがカムに押し付けられる力が減少すると、全体として摩擦損失が減少する。 ※カム半径が大きいと、バルブがカムに押し付けられる力が同じでも接触面の速度(m/s)が大きく摩擦損失(kgf)が大きくなるだけでなく、それ以上に摩擦損失トルク(kgf･m)が大きくなる。 　右下図は某社2リッター直列4気筒エンジンの摩擦損失が回転数によってどのように変化するかを示したものである（｢自動車用ガソリンエンジン設計の要諦｣（石川義和、山海堂2002)から引用)が、回転数上昇に伴い「動弁＆潤滑」の摩擦損失があまり変化せず、むしろ減少しているのはこの理由による（「潤滑」は回転数の上昇に伴い摩擦損失が増大するはずである)。 　なお、低回転で「動弁+潤滑」の摩擦損失が大きく増加しているのは、動弁系への潤滑油の供給が不十分になるからでもある。 　一方、デスモドロミックエンジンで、以下バルブスプリングが全くない状態（デスモドロミックであっても弱いバルブスプリングはある)を想定すると、FDは右上図で、 １ + 2 + 3 + 4 + 5 となる。図上では、バルブスプリングエンジンもデスモドロミックエンジンもFDに大差はない。しかし、回転数の増加に伴い１、2、3、4、5が増加する。つまりデスモドロミックエンジンではバルブスプリングエンジンと異なり、回転数上昇に伴い動弁系の摩擦損失が増大する。

さて、右及び右下の2図は上記引用元にあるドゥカティ・MOTO-GPレーサーエンジンのバルブ加速度である。青線が実測値、赤線がシミュレーション結果で、縦軸の加速度は回転数が変わっても同程度になるよう補正されているので目安と理解されたい。 　右図は比較的低回転時だが、加速度が細かく変動している。 　なお、加速度が変動するのはバルブ作動系が完全な剛体ではないためである。特にデスモドロミックエンジンでは、ロッカーアームの数が多い上に、閉ロッカーアーム（3つ上の図では「Negativi　rocker」）が長いため、 バルブスプリングエンジンよりバルブ作動系の剛性が低くなるのが欠点である。
そして高回転になると、右図のように本来、バルブが動かないはずの回転角であっても最大加速度の1割程度の加速度が生じている。 　このようにバルブ加速度は細かく変動するが、バルブスプリングエンジンでは、バルブ加速度の正負の一方はバルブがカムから浮く方向であるが、デスモドロミックエンジンでは、加速度の正負の両方でバルブが開・閉カムに押し付けられる。しかも開カムのリフトが小さい時でも閉カムのリフトは大きい。 　なお、縦軸は補正されているので、上図と最大加速度が同じように見えるが、仮に下図の回転数が上図の2倍とするなら、上図と対比すべき振幅は右図の4倍になる。 　このように見ていくと、最高出力発生回転域では、デスモドロミックエンジンのバルブ作動系摩擦損失はバルブスプリングエンジンより大きいとしか思えないのである。

本頁を公開したのは2008年7月だが、その後の補足は次のとおり。 補足１   MotoGP Technology Second edition (by Neil Spalding, Haynes2010)162頁に次の記述があり、ドゥカティも、デスモドロミックエンジンは高回転ではなく特に低中回転でのパワーロスが少ないとしている。 Filipo Preziosi, Director of Ducati Corse, commented on the advantages of the Desmo system used on his Desmosedici: 'There is ａ big difference with the Desmo system. It has less power requirements to move the valve, especially at low and intermediate revs. For sure, if you are not spending fuel to move the valves you can use the fuel to move the pistons. There is huge difference. Not at very high revs but at low and medium rpm. 　なお、この文の後に著者が次のようにも書いている。 Normal theory suggests the springs 'return' the energy as the valve goes back to its seat. While the energy may be returned, there is no doubt that compressing and releasing the springs will cause small fluctuations in crank speed as the crank drives the camshafts. The Ducati, therefore, not only has -smoothing benefits of being a 90°V4 but also an absence of valve spring loading and unloading. 　著者はデスモドロミックエンジンはバルブスプリングによる荷重変化（増加と減少）がないため、クランクシャフトの回転速度の変動が少ないとしている。デスモドロミックバルブ作動系であっても、バルブが上下に動く以上、加速度が働いており、作用反作用の法則によりカムシャフトに大きな力が加わることを理解していないようだ。理解しているなら「低中回転限定」であることを書くはずである。 補足2   「レーシングエンジン徹底研究」(林義正、1991グランプリ出版）に、デスモドロミックバルブ作動系についての次の記述がある。著名な技術者であっても間違えることはある。物事を印象、感覚で捉えて理解したつもりになることの怖さ、基本(この場合はニュートンの運動３法則)に立ち返って論理を積み上げることの重要性を痛感する。 　「第2の利点は、カム軸の回転変動がきわめて小さくなることだ。通常はバルブスプリングの強い反力を抑え込みながらカム面がバルブリフターをこじり下げるわけで、その抵抗によりカム軸は回転変動を起こしている。カム軸の回転角度で1度くらいの作動タイミングのずれは避けられないのが現状だ。デスモドロミック方式は、これが限りなくゼロに近くなる。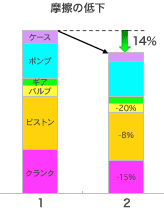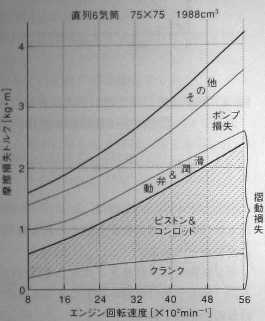」 　「第3の利点は、フリクションが大幅に減少することである。普通、シリンダーヘッドを組み上げた状態では、カム軸を回すのにかなりの力がいる。〜バルブスプリングの反力による抵抗が原因でそれがエンジンのパワーロスにもなる。デスモドロミック方式では、ヘッドを 組み上げた状態で、指先で簡単にカム軸を回せるのだ。かなりフリクションを小さくできるはずで、多気筒になるほど、高回転になるほど、このメリットは大きい。」 　「レーシングエンジンにデスモドロミック機構が採用されるのは時間の問題であると私は考えている。」 2022年12月3日追記 　その後、林氏は見解を改め「デスモドロミックバルブ作動系は高回転になるほど摩擦損失が増大する」としている(リンク)。

補足3   自動車技術会シンポジウム(2017.2.14）で「デスモドロミック，L型2気筒エンジンの過去，現在」（ドゥカティジャパン(株)　木下弘）と題する発表が行われた。右上図は発表資料中のグラフから私が数値を読み取り作成したもの。読取誤差はご容赦いただきたい。想定するエンジンは架空V8エンジンで、横軸は回転数(rpm/1000）、縦軸はバルブ作動系損失(kW)。 バルブ作動系損失の大きさ、20000rpmに到達する回転数からすると、2.4リットルF-1エンジンが想定されているようだ。  　回転上昇に伴い損失が急増しているのがデスモドロミックエンジンで、高回転域で損失が減少しているのがバルブスプリングエンジン。高回転域では損失がデスモドロミックエンジン＞バルブスプリングエンジンであることが分かる。    なお、最高回転数14000rpmのエンジンなら、デスモドロミックエンジンの方が損失が少ないと考えてはいけない。その回転数であれば、バルブスプリングエンジンのバルブスプリング荷重は小さく設定されるので、バルブスプリングエンジンの曲線は下に移動し、2曲線の交点は左に移動する。    右上図は損失出力を示しているので、次に損失トルク(クランクシャフト)を計算してみた。右中図において、横軸は回転数(rpm/1000)、縦軸はバルブ作動系損失トルク(Nm)で、点線がデスモドロミックエンジン、実線がバルブスプリングエンジン。   この曲線の近似式を元に、最高回転14000rpm、10000rpm、8000rpmのエンジンを想定し、損失トルクを計算したのが右下図である(「VSE2000」は「バルブスプリングエンジン/最高回転数20000rpm」）。 　近似式を基にした計算であるためイメージとして捉えていただきたいが、設定最高回転数によって設定バルブスプリング荷重が変わり、損失トルクも変わることが分ると思う。 　なお、ドゥカティジャパン（株）が公表したグラフは、あくまで一定の計算条件による試算であることに留意する必要がある。 2022年11月12日追記 　ドゥカティのウェブサイトでも「レーシングエンジンの動弁系として考えたとき、高回転域で摩擦損失が増大することがデスモドロミックの弱点」としている。デスモドロミック：伝統のエンジン機構がもたらすもの | DUCATI           MENU