小慣性トルクエンジンig-bang
1 4気筒エンジン
ビッグバン仮説を2007年に公開したが、当時、ネット、本、雑誌、ネットでは燃焼室内圧力によるトルク(以下「ガス圧トルク」)のみが注目されており、往復運動部の慣性力によるトルク(以下「慣性トルク」)については存在すら知られていない状態だった。このため、ビッグバン仮説では1次慣性力による慣性トルクについてのみ記述するだけで充分なものとして記事を書いた。
その後、ドゥカティの左右70度位相差90度V型4気筒(いわゆる「ツインパルス」エンジン)が登場したが、このレイアウトの採用理由は1次慣性力による慣性トルクでは説明できない。そこで、下の4気筒エンジンについて1次慣性力及び2次慣性力による慣性トルクTiを次式(近似式)により計算した。
Ti≒−mr2ω2(cosθ+(1/λ)cos2θ)×(sinθ+sin2θ/(2λ))
m:往復運動部質量
r:クランク半径(ストローク/2)
ω:クランクシャフト角速度
λ:コンロッド長/r(以下の計算では4とした)
mrω2cosθ:1次慣性力
mrω2(1/λ)cos2θ:2次慣性力
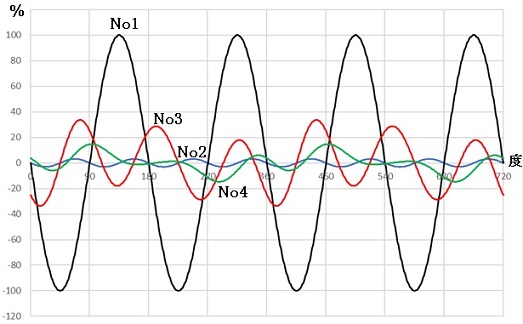
| No | 点火間隔 度 | 主要例 |
| 1 | 180-180-180-180 | ほとんどの4気筒エンジン |
| 2 | 90-180-270-180 | ヤマハYZR-M1(2004〜)、YZF-R1(2009〜)、180度クランク90度V型4気筒 |
| 3 | 90-270-90-270 | ホンダRVF750 |
| 4 | 90-200-90-340 | ドゥカティMoto GP、パニガーレV4 |
各エンジンの総排気量、往復運動部質量、ストローク/ボア比、コンロッド長、回転数は同じとし、No1エンジンの最大慣性トルクを100%として各エンジンの慣性トルクを示した。

No4エンジン(ドゥカティ左右70度位相差90度V型4気筒)は380度回転で4気筒の点火が終了するためガス圧トルク変動が注目されるが、No3エンジンより慣性トルク変動が小さく、スロットル開度変化によるガス圧トルク変化をライダーが感じやすくなる効果を狙ったものと思われる。ヤマハYZR-M1の不等間隔点火採用理由と同じである。
| No4エンジンの他のメリットとしてNo3エンジンより2次慣性力の不釣合いが小さくなることがある。 2次慣性力の釣合いだけなら90-180-90-360度点火の方がよいが、この場合、慣性トルクはNo4エンジンより大きなものになる。 |
240度等間隔点火並列3気筒と同排気量の並列4気筒エンジンの慣性トルクを比較してみる。
3気筒エンジンは4気筒エンジンと比べ
気筒あたり排気量 4/3倍
ストローク (4/3)1/3倍
往復運動部質量×ストローク (4/3)4/3倍
だが、レーシングエンジンでは最高回転数は気筒あたり排気量の(1/3乗)に反比例するので、慣性力は
(4/3)4/3 × (3/4)2/3=(4/3)2/3倍
これを加味して4気筒に対する3気筒の慣性トルクを百分率で示した。
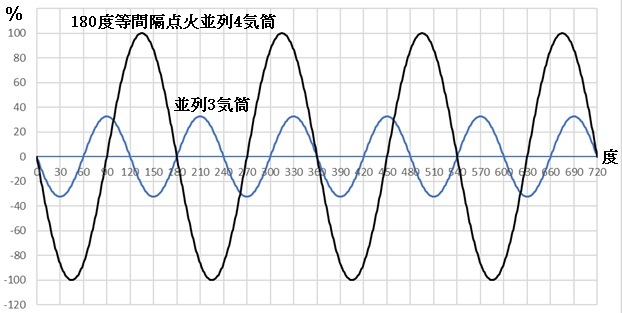
並列3気筒の最大慣性トルクは並列4気筒の34.5%に留まるし、気筒毎のガス圧トルクは3気筒の4/3倍なので、SN比(ガス圧トルク/慣性トルク)の差は大きい。
また、並列3気筒の慣性トルクは上記No2エンジン(いわゆるクロスプレーン並列4気筒)より大きいが、気筒毎のガス圧トルクは4気筒の4/3倍なので、SN比の差は慣性トルクの差から想像されるよりは小さくなる。
不等間隔点火エンジンのビッグバン効果の本質はその点火間隔ではなく慣性トルクの小ささにある。しかし、慣性トルクは小さいが等間隔点火である並列3気筒エンジンについて「ビッグバン」と表現するのは不適当だろう。今後はこれまで取りあげたエンジンを含め「小慣性トルクエンジン」と表現することにする。